Blind Search
Breadth-First
Search
Algoritma
Breadth-First Search (BFS) atau dikenal juga dengan nama algoritma pencarian
melebar adalah algoritma yang melakukan pencarian secara melebar yang
mengunjungi simpul secara preorder yaitu mengunjungi suatu simpul
kemudian mengunjungi semua simpul yang bertetangga dengan simpul tersebut
terlebih dahulu. Selanjutnya, simpul yang belum dikunjungi dan bertetangga
dengan simpulsimpul yang tadi dikunjungi , demikian seterusnya. Jika graf berbentuk
pohon berakar, maka semua simpul pada aras d dikunjungi lebih dahulu
sebelum simpul-simpul pad aras d+1.
Algoritma
ini memerlukan sebuah antrian q untuk menyimpan simpul yang telah
dikunjungi. Simpul-simpul ini diperlukan sebagai acuan untuk mengunjungi
simpul-simpul yang bertetanggaan dengannya. Tiap simpul yang telah dikunjungi
masuk ke dalam antrian hanya satu kali. Algoritma ini juga membutuhkan table
Boolean untuk menyimpan simpul yang telah dikunjungi sehingga tidak ada simpul
yang dikunjungi lebih dari satu kali.Breadth-first search (BFS) melakukan
proses searching pada semua node yang berada pada level atau hirarki yang sama
terlebih dahulu sebelum melanjutkan proses searching pada node di level
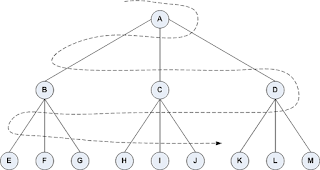
berikutnya. Urutan proses searching BFS ditunjukkan dalam Gambar 2.1 adalah:
A,B,C,D,E,F, ...
Cara Kerja
Algoritma BFS
Dalam
algoritma BFS, simpul anak yang telah dikunjungi disimpan dalam suatu antrian.
Antrian ini digunakan untuk mengacu simpul-simpul yang bertetangga dengannya
yang akan dikunjungi kemudian sesuai urutan pengantrian.Untuk memperjelas cara
kerja algoritma BFS beserta antrian yang digunakannya, berikut langkah-langkah
algoritma BFS:
1.
Masukkan simpul ujung (akar) ke dalam antrian.
2.
Ambil simpul dari awal antrian, lalu cek apakah simpul merupakan solusi.
3.
Jika simpul merupakan solusi, pencarian selesai dan hasil dikembalikan.
4.
Jika simpul bukan solusi, masukkan seluruh simpul yang bertetangga dengan
simpul tersebut (simpul anak) ke dalam antrian.
5.
Jika antrian kosong dan setiap simpul sudah dicek, pencarian selesai dan
mengembalikan hasil solusi tidak ditemukan.
6.
Ulangi pencarian dari langkah kedua.
Contohnya
terlihat dibawah ini:
Maka
penyelesaiannya adalah:Gambar (a) BFS(1): 1, 2, 3, 4, 5, 6, 7, 1.Gambar (b)
BFS(1): 1, 2, 3, 4, 5, 6, 7, 1Gambar (c) BFS(1): 1, 2, 3, 4, 5, 6, 7, 8, 9
Penerapan
BFS dalam Algoritma
Adapun
penerapan BFS pada algoritma adalah sebagai berikut:
Keuntungan
dan Kelemahan BFS
Keuntungan
dari BFS adalah :
* Tidak akan menemukan jalan buntu.
* Tidak ada satu solusi, maka BFS
search akan menemuknnya. Dan jika ada lebih dari satu solusi, maka solusi
minimum akan ditemukan.
Kelemahan
dari BFS adalah :
* Membutuhkan memori yang cukup
banyak, karena menyimpan semua node dalam satu pohon.
* Membutuhkan waktu yang cukup lama,
karena akan menguji n level untuk mendapatkan solusi pada level yang ke –(n+1).
2.5 Contoh kasus BFS
Berikut
adalah contoh kasus dengan menggunakan metode BFS. Kita akan mencari jalur
tujuan dengan menggunakan angkutan umum.Contoh :
Mencari
jalur angkutan umum dari terminal senen ke terminal Kp. Rambutan
* Initial State : Senen
* Goal State : Kp. Rambutan
RUTE
PERJALANAN
Penjelasan
Gambar :
- Membangkitakan anak dari terminal Senen = Terminal blok M, Terminal Pulo Gadung, Terminal Manggarai
- Karena goal state (Terminal Kp. Rambutan) belum tercapai maka kita bangkitkan anak dari terminal senen
Terminal
Blok M = Terminal Grogol, Terminal Lebak Bulus
Terminal
Lebak Bulus = Terminal Ciputat, Terminal Kp. Rambutan.
Terminal
Pulo Gadung = Terminal bekasi
Terminal
Manggarai = Terminal Cililitan, Terminal Harmoni
- Akhirnya tercapai Goal State (Terminal Kp. Rambutan).
Depth-first search
(DFS) adalah algoritma untuk melintasi atau mencari sebuah pohon , struktur pohon , atau grafik Satu dimulai pada akar (memilih beberapa node sebagai root dalam kasus
grafik) dan mengeksplorasi sejauh mungkin sepanjang masing-masing cabang
sebelum mundur .
Definisi formal
Secara formal, DFS adalah sebuah pencarian uninformed yang berlangsung dengan memperluas simpul anak
pertama dari pencarian pohon yang muncul dan dengan demikian akan semakin dalam sampai node tujuan
ditemukan, atau sampai hits node yang tidak memiliki anak. Kemudian pencarian backtracks , kembali ke node terakhir kebanyakan belum selesai menjelajahi. Dalam
implementasi non-rekursif, semua node yang baru diperluas ditambahkan ke stack untuk eksplorasi.
Para waktu dan ruang analisis DFS berbeda menurut wilayah penerapannya. Dalam ilmu komputer
teoretis, DFS biasanya digunakan untuk melintasi seluruh grafik, dan
membutuhkan waktu O (| V | + | E |) , linear dalam ukuran grafik. Dalam aplikasi ini juga menggunakan ruang O (| V |) dalam kasus terburuk untuk menyimpan tumpukan vertex di jalan pencarian
saat ini serta set-vertex sudah dikunjungi. Oleh karena itu, dalam pengaturan
ini, waktu dan batas ruang adalah sama seperti untuk luas pencarian pertama dan pilihan yang kedua algoritma untuk menggunakan
kurang tergantung pada kompleksitas dan lebih pada sifat-sifat yang berbeda
dari orderings titik dua algoritma menghasilkan.
Untuk aplikasi dari DFS untuk mencari masalah dalam kecerdasan buatan , Namun, grafik yang akan dicari sering terlalu besar untuk mengunjungi secara keseluruhan atau bahkan tak terbatas, dan DFS
mungkin menderita dari non-pemutusan kontrak kerja ketika panjang jalur di
pohon pencarian tak terbatas. Oleh karena itu, pencarian hanya dilakukan dengan
kedalaman terbatas, dan karena ketersediaan memori yang terbatas biasanya tidak
menggunakan struktur data yang melacak himpunan semua node yang sudah
dikunjungi sebelumnya. Dalam hal ini, waktu masih linier dalam jumlah vertex
diperluas dan tepi (walaupun nomor ini tidak sama dengan ukuran keseluruhan
grafik karena beberapa titik bisa dicari lebih dari sekali dan lain-lain tidak
sama sekali) tetapi ruang kompleksitas ini varian dari DFS hanya sebanding
dengan batas kedalaman, jauh lebih kecil daripada ruang yang dibutuhkan untuk
mencari sampai kedalaman yang sama dengan -pertama pencarian luas . Untuk aplikasi tersebut, DFS juga meminjamkan
sendiri jauh lebih baik untuk heuristik metode memilih cabang yang tampak mungkin. Ketika suatu batas kedalaman
yang tepat tidak diketahui apriori, pertama cari memperdalam
kedalaman-iteratif berlaku DFS berulang kali dengan urutan batas meningkat; dalam modus
kecerdasan buatan analisis, dengan faktor percabangan lebih besar dari satu, meningkatkan memperdalam
berulang kali berjalan dengan hanya faktor konstan selama kasus di mana batas
kedalaman yang benar dikenal karena pertumbuhan geometrik jumlah node per
tingkat.
pencarian mendalam-pertama mulai dari A, dengan asumsi bahwa tepi kiri
dalam grafik ditunjukkan dipilih sebelum tepi kanan, dan dengan asumsi
pencarian sebelumnya-ingat node dikunjungi dan tidak akan mengulangi mereka
(karena ini
adalah grafik kecil), akan mengunjungi node dalam urutan sebagai berikut:
A, B, D, F, E, C, G.
Melakukan pencarian yang sama tanpa mengingat hasil sebelumnya mengunjungi
node dalam mengunjungi node dalam urutan A,
B
, D, F, E, A, B, D, F
, E, dll selamanya, terperangkap dalam A, B, D, F , E siklus dan tidak
pernah mencapai C atau G.
Iteratif memperdalam mencegah loop ini dan akan mencapai node berikut pada
kedalaman berikut, dengan asumsi itu hasil dari kiri-ke-kanan seperti di atas:
- 0: A
- 1: A (diulang), B, C, E
(Perhatikan bahwa iterasi memperdalam sekarang melihat C, ketika sebuah
pencarian depth-first konvensional tidak.)
- 2: A B,, D, F, C, G, E, F
(Perhatikan bahwa masih melihat C, tetapi itu datang belakangan juga
diketahui bahwa melihat E melalui jalan yang berbeda, dan loop kembali ke F dua
kali..)
- 3: A B,, D, F, E, C, G, E, F, B
Untuk grafik ini, kedalaman lebih yang ditambahkan, dua siklus
"ABFE" dan "AEFB" hanya akan mendapatkan lagi sebelum
algoritma menyerah dan mencoba cabang lain.
Alam sebagian besar hasil pencarian pertama kedalaman grafik (jika
dianggap sebagai fungsi daripada prosedur ) adalah pohon rentang dari vertex mencapai selama pencarian. Berdasarkan pohon rentang,
tepi grafik asli dapat terbagi menjadi tiga kelas: tepi depan, yang
titik dari simpul pohon itu untuk salah satu keturunannya, kembali tepi,
yang titik dari simpul ke salah satu dari nenek moyangnya, dan tepi salib,
yang tidak melakukan keduanya. Kadang-kadang pohon tepi, pinggiran yang
termasuk ke dalam pohon rentang itu sendiri, yang diklasifikasikan secara
terpis
ah dari tepi ke depan. Dapat ditunjukkan bahwa jika grafik ini
tidak diarahkan maka semua ujungnya adalah ujung atau tepi-tepi pohon kembali.
orderings Vertex
Hal ini juga memungkinkan untuk menggunakan pencarian depth-first order yang linier titik dari grafik asli (atau pohon). Terdapat tiga cara yang umum untuk melakukan hal ini:- preordering adalah daftar vertex dalam urutan yang pertama kali dikunjungi oleh algoritma pencarian pertama yang mendalam. Ini adalah cara yang kompak dan alam menggambarkan kemajuan pencarian, seperti yang dilakukan sebelumnya di artikel ini. Sebuah preordering pohon ekspresi adalah ekspresi dalam notasi Polandia .
- postordering adalah daftar vertex dalam urutan bahwa mereka terakhir dikunjungi oleh algoritma. Sebuah postordering sebuah pohon ekspresi adalah ekspresi dalam notasi Polandia terbalik .
- Sebuah postordering reverse kebalikan dari postordering sebuah, yaitu daftar vertex dalam urutan sebaliknya dari kunjungan terakhir mereka. Saat mencari pohon, postordering reverse adalah sama dengan preordering, namun secara umum mereka berbeda saat mencari grafik. Sebagai contoh, ketika mencari grafik diarahkan
mulai dari A node, mengunjungi salah satu simpul secara berurutan, untuk
menghasilkan daftar baik ABDBACA, atau ACDCABA (tergantung pada algoritma
memilih untuk mengunjungi B atau C pertama). Perhatikan bahwa ulangi dilihat
dalam bentuk mundur ke node, untuk memeriksa apakah masih belum dikunjungi
tetangga, termasuk di sini (bahkan jika ditemukan memiliki none). Jadi
preorderings mungkin adalah ABDC dan ACDB (urutan oleh kejadian paling kiri
node dalam daftar di atas), sedangkan sebaliknya postorderings mungkin adalah
ACBD dan ABCD (urutan oleh kejadian paling kanan node dalam daftar di atas).
Reverse postordering menghasilkan penyortiran topologi dari setiap grafik asiklik diarahkan . Memesan ini juga
bermanfaat dalam analisis aliran kontrol karena sering kali
merupakan Linearisasi alami aliran kontrol. Grafik di atas mungkin merupakan aliran
kontrol dalam sebuah fragmen kode seperti
jika (A), (
B
) Else (
C
)
D
dan wajar
untuk mempertimbangkan kode ini dalam urutan ABCD atau ACBD, tetapi tidak alami
untuk menggunakan perintah ABDC atau ACD B.
Daftar Pustaka :








Komentar
Posting Komentar