Fuzzy Logic

Fuzzy Logic


Soft Computing merupakan inovasi baru dalam membangun sistem cerdas. Sistem cerdas ini merupakan sistem yang memiliki keahlian seperti manusia pada domain tertentu, mampu beradaptasi dan belajar agar dapat bekerja lebih baik jika terjadi perubahan lingkungan. Unsur-unsur pokok dalam Soft Computing adalah : Sistem fuzzy, Jaringan Saraf Tiruan, Probabilistic Reasoning, Evolutionary Computing.
Sistem fuzzy secara umum terdapat 5 langkah dalam melakukan penalaran, yaitu:
1.      Memasukkan input fuzzy.
2.      Mengaplikasikan operator fuzy.
3.      Mengaplikasikan metode implikasi.
4.      Komposisi semua output.
5.      Defuzifikasi.

Logika Fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input ke dalam ruang output. Untuk sistem yang sangat rumit, penggunaan logika fuzzy (fuzzy logic) adalah salah satu pemecahannya. Sistem tradisional dirancang untuk mengontrol keluaran tunggal yang berasal dari beberapa masukan yang tidak saling berhubungan.  Karena ketidaktergantungan ini, penambahan masukan yang baru akan memperumit proses kontrol dan membutuhkan proses perhitungan kembali dari semua fungsi . Kebalikannya, penambahan masukan baru pada sistem fuzzy, yaitu sistem yang bekerja berdasarkan prinsip-prinsip logika fuzzy, hanya membutuhkan penambahan fungsi keanggotaan yang baru dan aturan-aturan yang berhubungan dengannya.
Secara umum, sistem fuzzy sangat cocok untuk penalaran pendekatan terutama untuk sistem yang menangani masalah-masalah yang sulit didefinisikan dengan menggunakan model matematis Misalkan, nilai masukan dan parameter sebuah sistem bersifat kurang akurat atau kurang jelas, sehingga sulit mendefinisikan model matematikanya.
Sistem fuzzy mempunyai beberapa keuntungan bila dibandingkan dengan sistem tradisional, misalkan pada jumlah aturan yang dipergunakan. Pemrosesan awal sejumlah besar nilai menjadi sebuah nilai derajat keanggotaan pada sistem fuzzy mengurangi jumlah nilai menjadi sebuah nilai derajat keanggotaan pada sistem fuzzy mengurangi jumlah nilai yang harus dipergunakan pengontrol untuk membuat suatu keputusan. Keuntungan lainnya adalah sistem fuzzy mempunyai kemampuan penalaran yang mirip dengan kemampuan penalaran manusia. Hal ini disebabkan karena sistem fuzzy mempunyai kemampuan untuk memberikan respon berdasarkan informasi yang bersifat kualitatif, tidak akurat, dan ambigu.
Ada beberapa alasan penggunaan Logika Fuzzy :
1.      Logika Fuzzy sangat fleksibel.
2.      Logika Fuzzy memiliki toleransi.
3.      Konsep logika fuzzy mudah dimengerti. Konsep matematis yang mendasari penalaran fuzzy sangat sederhana dan mudah dimengerti.
4.      Logika fuzzy mampu memodelkan fungsi-fungsi nonlinear yang sangat kompleks.
5.      Logika fuzzy dapat membangun dan mengaplikasikan pengalaman-pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan.
6.      Logika fuzzy dapat bekerjasama dengan teknik-teknik kendali secara konvensional.
7.      Logika fuzzy didasarkan pada bahasa alami.(Sri Kusumadwi,2002:3)

Sistem fuzzy pertama kali diperkenalkan oleh Prof. L. A. Zadeh dari Barkelay pada tahun 1965. Sistem fuzzy merupakan penduga numerik yang terstruktur dan dinamis. Sistem ini mempunyai kemampuan untuk mengembangkan sistem intelijen dalam lingkungan yang tak pasti. Sistem ini menduga suatu fungsi dengan logika fuzzy. Dalam logika fuzzy terdapat beberapa proses yaitu penentuan himpunan fuzzy, penerapan aturan IF-THEN dan proses inferensi fuzzy (Marimin, 2005:10).

Ada beberapa metode untuk merepresentasikan hasil logika fuzzy yaitu metode Tsukamoto, Sugeno dan Mamdani. Pada metode Tsukamoto, setiap konsekuen direpresentasikan dengan himpunan fuzzy dengan fungsi keanggotaan monoton. Output hasil inferensi masing-masing aturan adalah z,  berupa himpunan biasa (crisp) yang ditetapkan berdasarkan -predikatnya. Hasil akhir diperoleh dengan menggunakan rata-rata terbobotnya.(Sri Kusumadewi,2002:108)
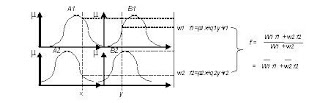
Metode Sugeno mirip dengan metode Mamdani, hanya output (konsekuen) tidak berupa himpunan fuzzy, melainkan berupa konstanta atau persamaan liniar. Ada dua model metode Sugeno yaitu model fuzzy sugeno orde nol dan model fuzzy sugeno orde satu. Bentuk umum model fuzzy sugeno orde nol adalah :

IF (x1 is A1) o (x2 is A2) o ….. o (xn is An) THEN  z = k

Bentuk umum model fuzzy Sugeno orde satu adalah :
IF (x1 is A1) o (x2 is A2) o ….. o (xn is An) THEN  z = p1.x1 + … pn.xn + q
Defuzzifikasi pada metode Sugeno dilakukan dengan mencari nilai rata-ratanya.

 Gambar 1  Model fuzzy sugeno orde 1
Pada metode Mamdani, aplikasi fungsi implikasi menggunakan MIN, sedang komposisi aturan menggunakan metode MAX. Metode Mamdani dikenal juga dengan metode MAX-MIN.  Inferensi output yang dihasilkan berupa bilangan fuzzy maka harus ditentukan suatu nilai crisp tertentu sebagai output. Proses ini dikenal dengan defuzzifikasi. Ada beberapa tahapan untuk mendapatkan output yaitu:

A. Pembentukan himpunan fuzzy
Pada metode Mamdani baik variabel input maupun variabel output dibagai menjadi satu atau lebih himpunan fuzzy.
2.      Aplikasi fungsi implikasi
Pada metode Mamdani, fungsi implikasi yang digunakan adalah Min.
3.      Komposisi Aturan
Tidak seperti penalaran monoton, apabila sistem terdiri dari beberapa aturan, maka inferensi diperoleh dari kumpulan dan korelasi antar aturan. Ada 3 metode yang digunakan dalam melakukan inferensi sistem fuzzy yaitu : Max, Additive dan Probabilistik OR
a.Metode Max (Maximum)
Pada metode ini solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy dan mengaplikasikan ke output dengan menggunakan operator OR(union). Jika semua proposisi telah dievaluasi, maka output akan beisi suatu himpunan fuzzy yang merefleksikan konstribusi dari tiap-tiap proposisi. Secara umum dapat dituliskan :
µsf[xi] ← max ( µsf[xi] , µkf[xi])
dengan :
µsf[xi]=nilai keanggotaan solusi fuzzy sampai aturan ke-i
µkf[xi]=nilai keanggotaan konsekuen fuzzy aturan ke-i
b. Metode Additive (Sum)
Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan bounded-sumterhadap semua output dareah fuzzy. Secara umum dituliskan:
µsf[xi] ← max ( 1, µsf[xi]  + µkf[xi] )
µsf[xi]=nilai keanggotaan solusi fuzzy sampai aturan ke-i
µkf[xi]=nilai keanggotaan konsekuen fuzzy aturan ke-i
c. Metode Probabilistik OR
Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan product terhadap semua output daerah fuzzy. Secara umun dituliskan :
µsf[xi] ← max ( µsf[xi]  + µkf[xi] ) – (µsf[xi]  * µkf[xi] )
µsf[xi]=nilai keanggotaan solusi fuzzy sampai aturan ke-i
µkf[xi]=nilai keanggotaan konsekuen fuzzy aturan ke-i
4.      Penegasan /Defuzzifikasi

Input dari proses Defuzzifikasi adalah suatu himpunan fuzzy yang diperoleh dari komposisi aturan-aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu bilangan pada domain himpunan fuzzy tersebut. Sehingga jika diberikan suatu himpunan fuzzy dalam range tertentu, maka harus dapat diambil suatu nilai crisp tertentu sebagai output.
Ada beberapa metoda yang dipakai dalam defuzzifikasi:
a. Metode Centroid.
Pada metode ini penetapan nilai crisp dengan cara mengambil titik pusat daerah fuzzy.
b. Metode Bisektor.
Pada metode ini , solusi crisp diperoleh dengan cara mengambil nilai pada domain fuzzy yang memiliki nilai keanggotaan seperti dari jumlah total nilai keanggotaan pada daerah fuzzy.
c. Metode Means of Maximum (MOM).
Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai rata-rata domain yang memiliki niali keanggotaan maksimum.
d. Metode Largest of Maximum (LOM)
Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai terbesar dari domain yang memiliki niali keanggotaan maksimum.
e. Metode Smallest of Maksimum (SOM).
Solusi crisp diperoleh dengan cara mengambil nilai terkecil dari domain yang memiliki nilai keanggotaan maksimum.


Penerapan Logika Fuzzy pada Sistem Pengaturan Lampu Lalulintas

Logika fuzzy dalam pengaturan lampu lalulintas amat diperlukan untuk memperlancar arus lalulintas. Dengan adanya system yang bekerja secara otomatis diharapkan angka kecelakaan yang disebabkan oleh masalah lampu lalulintas dapat berkurang. Selain itu dengan adanya lampu lalulintas yang otomatis tentu saja akan mengurangi tugas polisi lalulintas, sehingga mereka bisa mengerjakan hal-hal lain yang belum teratasi.
Sedangkan sebagai dasar pengendalian dari sistem yang dijalankan, digunakan algoritma logika fuzzy. Untuk memudahkan pengendalian lampu lalulintas, ada beberapa istilah yang digunakan dalam pengendaliannya antara lain :
  • Untuk kepadatan jumlah kendaraan adalah :
–         Tidak Padat (TP),
–         Kurang Padat (KP),
–         Cukup Padat (CP),
–         Padat (P) dan
–         Sangat Padat (SP).
  • Sedangkan untuk lama nyala lampu adalah :
–         Cepat (C),
–         Agak Cepat (AC),
–         Sedang (S),
–         Agak Lama (AL) dan
–         Lama (L).
Jelas istilah-istilah tersebut dapat menimbulkan makna ganda (ambiguity) dalam pengertiannya. Logika Fuzzy dapat mengubah makna ganda tersebut ke dalam model matematis sehingga dapat diproses lebih lanjut untuk dapat diterapkan dalam sistem kendali.
Untuk menyelesaikan masalah tersebut digunakan teori himpunan Fuzzy, logika bahasa dapat diwakili oleh sebuah daerah yang mempunyai jangkauan tertentu yang menunjukkan derajat keanggotaannya (fungsi keanggotaan). Untuk kasus disini, sebut saja derajat keanggotaan itu adalah u(x) untuk x adalah jumlah kendaraan.


http://socs.binus.ac.id/2012/03/02/pemodelan-dasar-sistem-fuzzy/  

Komentar

Posting Komentar

Postingan populer dari blog ini

Negara Belgia

Gambar
ILMU SOSIAL DASAR Nama : Rizky Noer Muhammad Kelas : 1 KA 37 NPM : 19114707 Jurusan : Sistem Informasi Mata Kuliah : ISD ( Ilmu Sosial Dasar ) Belgia Belgia (secara resmi disebut Kerajaan Belgia ) adalah sebuah negara yang terletak di bagian barat benua Eropa. Negara ini merupakan negara anggota pendiri Uni Eropa dan menjadi ibukota Uni Eropa, serta organisasi internasional lainnya termasuk NATO. Belgia meliputi wilayah seluas 30.528 km² dan memiliki populasi penduduk sekitar 10,5 juta jiwa. Terletak di antara dua perbatasan budaya antara daerah Jermanik dan Latin, Belgia adalah sebuah negara dari dua kelompok etnik, Flandria dan Perancis, yang mana sebagian besarnya adalah Walloon dan sekelompok kecil adalah pembicara bahasa Jerman. Dari tinjauan Geografis, dua area terbesar dari Belgia adalah wilayah penutur bahasa Belanda yang merupakan area dari Flandria yang ada di utara, dengan 59% dari populasi secara keseluruhan, dan wilayah penutur bahasa Perancis ter...
Baca selengkapnya

Budaya Organisasi, Tipe Kepemimpinan & Strategi Organisasi

Pengertian dan Fungsi Budaya Organisasi  Budaya organisasi adalah sebuah sistem makna bersama yang dianut oleh para anggota yang membedakan suatu organisasi dari organisasi-organisasi lainnya. Sistem makna bersama ini adalah sekumpulan karakteristik kunci yang dijunjung tinggi oleh organisasi. Budaya organisasi sebagai istilah deskriptif Budaya organisasi berkaitan dengan bagaimana karyawan memahami karakteristik budaya suatu organisasi, dan tidak terkait dengan apakah karyawan menyukai karakteristik itu atau tidak. Budaya organisasi adalah suatu sikap deskriptif, bukan seperti kepuasan kerja yang lebih bersifat evaluatif. Penelitian mengenai budaya organisasi berupaya mengukur bagaimana karyawan memandang organisasi mereka:     Apakah mendorong kerja tim?     Apakah menghargai inovasi?     Apakah menekan inisiatif? Sebaliknya, kepuasan kerja berusaha mengukur respons afektif terhadap lingkungan kerja, seperti bagaima...
Baca selengkapnya

Blind Search

Gambar
Breadth-First Search Algoritma Breadth-First Search (BFS) atau dikenal juga dengan nama algoritma pencarian melebar adalah algoritma yang melakukan pencarian secara melebar yang mengunjungi simpul secara preorder yaitu mengunjungi suatu simpul kemudian mengunjungi semua simpul yang bertetangga dengan simpul tersebut terlebih dahulu. Selanjutnya, simpul yang belum dikunjungi dan bertetangga dengan simpulsimpul yang tadi dikunjungi , demikian seterusnya. Jika graf berbentuk pohon berakar, maka semua simpul pada aras d dikunjungi lebih dahulu sebelum simpul-simpul pad aras d +1. Algoritma ini memerlukan sebuah antrian q untuk menyimpan simpul yang telah dikunjungi. Simpul-simpul ini diperlukan sebagai acuan untuk mengunjungi simpul-simpul yang bertetanggaan dengannya. Tiap simpul yang telah dikunjungi masuk ke dalam antrian hanya satu kali. Algoritma ini juga membutuhkan table Boolean untuk menyimpan simpul yang telah dikunjungi sehingga tidak ada simpul yang dikunjungi lebih d...
Baca selengkapnya